
A Heap is a special Tree-based data structure in which the tree is a complete binary tree. Generally, Heaps can be of two types: Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree. Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
Applications of Heaps
Heap Data Structure is generally taught with Heapsort. Heapsort algorithm has limited uses because Quicksort is better in practice. Nevertheless, the Heap data structure itself is enormously used. Following are some uses other than Heapsort.
Priority Queues
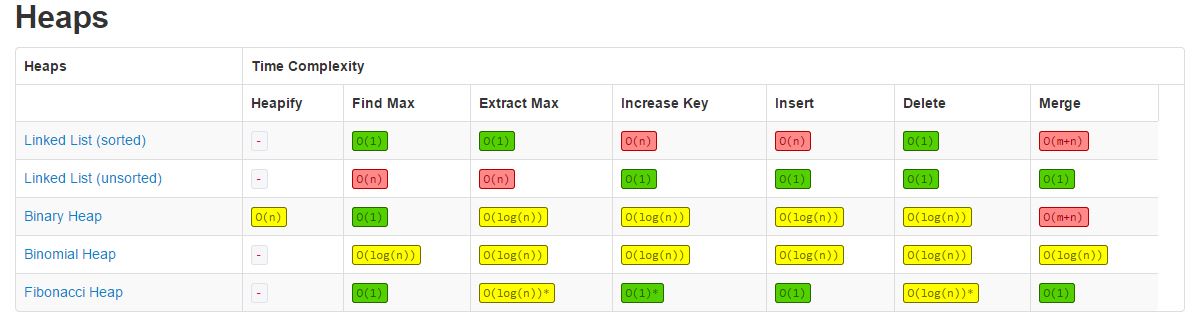
Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time. Binomoial Heap and Fibonacci Heap are variations of Binary Heap. These variations perform union also in O(logn) time which is a O(n) operation in Binary Heap. Heap Implemented priority queues are used in Graph algorithms like Prim’s Algorithm and Dijkstra’s algorithm.The Heap data structure can be used to efficiently find the kth smallest (or largest) element in an array.
